Perimeter:
The length of the boundary of a closed figure is called the perimeter of the plane figure. The units of perimeter are same as that of length, i.e., m, cm, mm, etc.
Area:
A part of the plane enclosed by a simple closed figure is called a plane region and the measurement of plane region enclosed is called its area.
Area is measured in square units
Perimeter and Area of Rectangle:
● The perimeter of rectangle = 2(l + b).
● Area of rectangle = l × b; (l and b are the length and breadth of rectangle)
● Diagonal of rectangle = √(l² + b²)
Perimeter and Area of the Square:
● Perimeter of square = 4 × S.
● Area of square = S × S.
● Diagonal of square = S√2; (S is the side of square)
Perimeter and Area of the Triangle:
● Perimeter of triangle = (a + b + c); (a, b, c are 3 sides of a triangle)
● Area of triangle = √(s(s - a) (s - b) (s - c)); (s is the semi-perimeter of triangle)
● S = 1/2 (a + b + c)
● Area of triangle = 1/2 × b × h; (b base , h height)
● Area of an equilateral triangle = (a²√3)/4; (a is the side of triangle)
Perimeter and Area of the Parallelogram:
● Perimeter of parallelogram = 2 (sum of adjacent sides)
● Area of parallelogram = base × height
Perimeter and Area of the Rhombus:
● Area of rhombus = base × height
● Area of rhombus = 1/2 × length of one diagonal × length of other diagonal
● Perimeter of rhombus = 4 × side
Perimeter and Area of the Trapezium:
● Area of trapezium = 1/2 (sum of parallel sides) × (perpendicular distance between them)
= 1/2 (p₁ + p₂) × h (p₁, p₂ are 2 parallel sides)
Circumference and Area of Circle:
● Circumference of circle = 2πr
= πd
Where, π = 3.14 or π = 22/7
r is the radius of circle
d is the diameter of circle
● Area of circle = πr²
● Area of ring = Area of outer circle - Area of inner circle.
The formula of perimeter and area of square are explained step-by-step with solved examples.
If 'a' denotes the side of the square, then, length of each side of a square is 'a' units
perimeter and area of square
Perimeter of square = AB + BC + CD + DA
= (a + a + a + a) units
= 4a units
● Perimeter of the square = 4a units
We know that the area of the square is given by
Area = side × side
A = a × a sq. units
Therefore, A = a² square units
Therefore, a² = A Here, a is the side of the square.
Therefore, a² = √A
Therefore, side of the square = √Area
● Side of the square = P/4 units
● Area of the square = a × a = (P/4)² sq. units
● Area of square = 1/2 × (diagonal)² sq. units
● Length of the diagonal = √(a² + a²) = √(2a²^2) = a√2 units
Worked-out examples on Perimeter and Area of the Square:
1. Find the perimeter and area of a square of side 11 cm.
Solution:
We know that the perimeter of square = 4 × side
Side= 11 cm
Therefore, perimeter = 4 × 11 cm = 44 cm
Now, area of the square = (side × side) sq. units
= 11 × 11 cm²
= 121 cm²
2. The perimeter of a square is 52 m. Find the area of the square.
Solution:
Perimeter of square = 52 m
But perimeter of square = 4 × side
Therefore, 4 × side = 52 m
Therefore, side= 52/4 m = 13m
Now, the area of the square = (side × side)
Therefore, area of the square = 13 × 13 m² = 169 m².
3. The area of a square is 144 m². Find its perimeter.
Solution:
Area of square = side × side
Given; area of square = 144 m²
Therefore, side² = 144 m²
Therefore, side = √(144 m²) = √(2 × 2 × 2 × 2 × 3 × 3) m² = 2 × 2 × 3 m = 12 m
Now, the perimeter of the square = 4 x side = 4 × 12 m = 48 m
4. The length of the diagonal of a square is 12 cm. Find its area and perimeter.
Solution:
Diagonal of a square = 12 cm
Area of square = 1/2 (d)²
= 1/2 (12)²
= 1/2 × 12 × 12
= 72
Side of a square = √Area
= √72
= √(2 × 2 × 2 × 3 × 3)
= 2 × 3√2
= 6 × 1.41
= 8.46 cm
Perimeter of square = 4 × 8.46 = 33.84 cm
5. The perimeter of a square courtyard is 144 m. Find the cost of cementing it at the rate of $5 per m².
Solution:
Perimeter of square courtyard = 144 m
Therefore, side of the square courtyard = 144/4 = 36 m
Therefore, area of square courtyard = 36 × 36 m² = 1296 m²
For 1 m², the cost of cementing = $5
For 1296 m², the cost of cementing = $1296 × 5 = $6480
The above solved examples are explained how to solve perimeter and area of square with the detailed explanation.
Worked-out examples on Area of the Path:
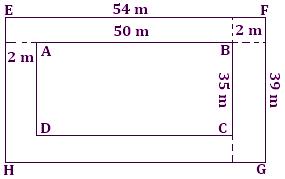
1. A rectangular lawn of length 50 m and breadth 35 m is to be surrounded externally by a path which is 2 m wide. Find the cost of turfing the path at the rate of $3 per m².
Solution:
Length of the lawn = 50 m
Breadth of the lawn = 35 m
Area of the lawn = (50 × 35) m²
= 1750 m²
cmLength of lawn including the path = [50 + (2 + 2)] m = 54 cm
Breadth of the lawn including the path = [35 + (2 + 2)] m = 39 m
Area of the lawn including the path = 54 × 39 m² = 2106 m²
Therefore, area of the path = (2106 - 1750) m² = 356 m²
For 1 m², the cost of turfing the path = $ 3
For 356 m², the cost of turfing the path = $3 × 356 = $1068
2. A painting is painted on a cardboard 19 cm and 14 cm wide, such that there is a margin of 1.5 cm along each of its sides. Find the total area of the margin.
Solution:
Length of the cardboard = 19 cm
Breadth of the cardboard = 14 cm
Area of the cardboard = 19 × 14 cm² = 266 cm²
Length of the painting excluding the margin = [19 - (1.5 + 1.5)] cm = 16 cm
Breadth of the painting excluding the margin = 14 - (1.5 + 1.5) = 11 cm
Area of the painting excluding the margin = (16 × 11) cm² = 176 cm²
Therefore, area of the margin = (266 - 176) cm² = 90 cm²
3. A square flowerbed is surrounded by a path 10 cm wide around it. If the area of the path is 2000 cm², find the area of the square flower-bed.
Solution:
In the adjoining figure,
ABCD is the square flowerbed.
EFGH is the outer boundary of the path.
Let each side of the flowerbed = x cm
Then, the area of the square flowerbed ABCD (x × x) cm² = x² cm²
Now, the side of the square EFGH = (x + 10 + 10) cm = (x + 20) cm
Therefore, area of the path = Area of EFGH - Area of ABCD
= [(x + 20)² - x²] cm²
= [x² + 400 + 40x - x²] cm² = (40x + 400) cm²
But the area of path given = 2000 cm²
Therefore, 40x + 400 = 2000
⟹ 40x = 2000 - 400
⟹ 40x = 1600
⟹ x = 1600/40 = 40
Therefore, side of square flowerbed =40 cm
Therefore, the area of the square flowerbed = 40 × 40 cm² = 1600 cm²
1600
Therefore, area of the path = Area of EFGH - Area of ABCD
= [(x + 20)² - x²] cm²
= [x² + 400 + 40x - x²] cm² = (40x + 400) cm²
But the area of path given = 2000 cm²
Therefore, 40x + 400 = 2000
⟹ 40x = 2000 - 400
⟹ 40x = 1600
⟹ x = 1600/40 = 40
Therefore, side of square flowerbed =40 cm
Therefore, the area of the square flowerbed = 40 × 40 cm² = 1600 cm²
By- Prof. Rakesh Giri......


कोई टिप्पणी नहीं:
एक टिप्पणी भेजें